top of page


Bridge Design and Building
A resource for Clifton State High School
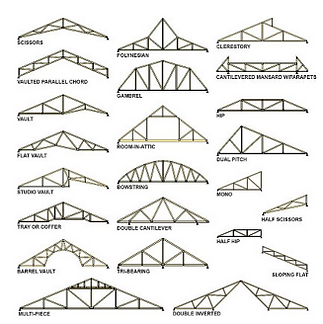

Using Pythagoras in Roof Trusses - Medium
We can use mathematical rules to work out side lengths in right angle triangles.
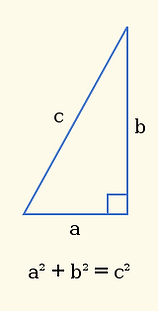
Pythagoras' rule desribes how the lengths of the sides of a
right angle triangle are related to each other.
side c is always the longest side and opposite the right angle
sides a and b are interchangeable (they can be swapped)
To find c, use:
To find b, use:
To find a, use:
If you look at the formulas to find a or b, they are basically the same, except the a and b are swapped in each.
Task 1
Go to the "Parts of a Roof Truss" to see what each part does.
Task 2
Answer the following questions:
1. Consider the Kingpost roof truss design below.
If the height of the roof needs to be 3 m and the nominal span needs to be 10 m, not including overhang, how long will the top chords need to be?
2. Consider the Howe roof truss below.
a) How many right angle triangles are there?
b) How many triangles are there?
c) Classify each triangle using sides and angles as you did in the previous activity about types of triangles.
d) If a top chord is 5 m long and the nominal span is 12 m, how high is the roof?
e) If a vertical web member is placed one quarter of the way along bottom chord, how far along the top chord will it be? Halfway? Explain by modelling.
3.

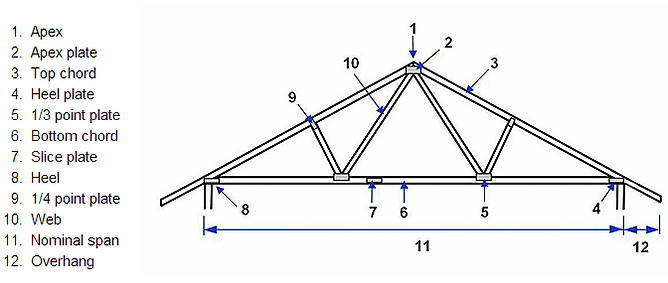

vertical web member
Centre post
top chord
bottom of page








